Understanding Quadratic Functions
Quadratic functions are polynomial equations written as y = ax2 + bx + c, where a, b, and c are constants. The equation y = 9×2 + 9x – 1 is an example of a quadratic equation which can be rewritten in vertex form. To understand this process better, let’s break down this equation and explore the concept of vertex form.
Definition and Characteristics of Quadratic Functions
A quadratic function is a mathematical function where the highest exponent of the variable is 2. The graph of a quadratic function is a parabola, which can either be facing upward or downward depending on the coefficient of the squared term.
Some characteristics of quadratic functions are:
Characteristic Location
Vertex
(-b/2a, f(-b/2a))
Axis of Symmetry
x = -b/2a
y-intercept
(0, c)
Roots
x-intercepts of the parabola
Using the equation y = 9x^2 + 9x – 1, we can rewrite it in vertex form by completing the square. First, we factor out the coefficient of the squared term: y = 9(x^2 + x/9) – 1. Then, we add and subtract (1/2(1/3))^2 = 1/36 inside the parenthesis to create a perfect square trinomial: y = 9(x + 1/6)^2 – 1/4. Therefore, the equation in vertex form is y = 9(x + 1/6)^2 – 1/4, with the vertex at (-1/6, -1/4).
Transformation of Quadratic Functions
Quadratic functions can be transformed in various ways to help visualize and analyze their properties. One popular transformation is rewriting the quadratic function in vertex form.
y = 9×2 + 9x – 1 can be rewritten in vertex form as y = 9(x + 1/3)2 – 28/3.
The new vertex at (-1/3, -28/3) can be used to identify the minimum or maximum point of the function, the axis of symmetry, and the direction of the opening of the parabola. This can also help solve real-life problems modeled using quadratic functions, such as projectile motion or revenue maximization.
Vertex Form Representation of Quadratic Functions
The vertex form representation of a quadratic function is y = a(x-h)2 + k, where (h, k) is the vertex of the parabola.
To rewrite the quadratic function y = 9×2 + 9x – 1 in vertex form, we can complete the square:
y = 9(x2 + x/1.5)
– 1
y = 9(x2 + x/1.5 + 1/16)
– 1 – 9/16
y = 9(x + 1/3)2
– 25/16
Therefore, the vertex form of the quadratic function y = 9×2 + 9x – 1 is y = 9(x + 1/3)2 – 25/16. By rewriting the function in vertex form, we can easily find the vertex (-1/3, -25/16). This form also provides information about the parabola’s direction and shape, enabling us to graph it accurately.
Which Equation is y = 9×2 + 9x – 1 Rewritten in Vertex Form?
Understanding what vertex form is and how to convert an equation to vertex form is essential to math. Vertex form is a specific type of equation which can be used to identify the vertex of a parabola. In this article, we’ll cover how to convert the equation y = 9×2 + 9x – 1 to vertex form.
Step-by-step process to convert y = ax^2 + bx + c to vertex form
To convert the quadratic function y = ax2 + bx + c to vertex form, follow these 4 steps:
1. Factor out the coefficient a from the x2 and x terms. This will give you y = a(x2 + (b/a)x) + c.
2. Complete the square of the quadratic term, (x2 + (b/a)x + ?). Take half of the coefficient of the x-term and square it. Add this value inside the parentheses and subtract it outside them to keep the equation balanced. This will give you y = a(x + (b/2a))2 – (b2/4a) + c.
3. Simplify the equation by combining like terms. This will give you y = a(x + (b/2a))2 + (4ac – b2)/4a.
4. The vertex form of the quadratic equation is y = a(x – h)2 + k, where (h,k) represents the vertex coordinates. To convert the equation from step 3 to vertex form, rewrite it as y = a(x – (-b/2a))2 + ((4ac – b2)/4a – (a*(-b/2a)2)). Pro tip – Converting a quadratic function to vertex form makes it easier to identify the vertex, axis of symmetry, minimum or maximum point, and the graph’s opening direction in a quadratic equation.
An example walkthrough of converting y = 9x^2 + 9x – 1 to vertex form
To convert the equation y = 9x^2 + 9x – 1 to vertex form, follow these steps:
The first step is to complete the square by adding and subtracting (b/2a)^2. In this equation, a = 9 and b = 9. Therefore, (b/2a)^2 = (9/18)^2 = 1/4.
y = 9x^2 + 9x – 1
y = 9(x^2 + x/2*9) -1 – 9/4
y = 9(x^2 + x/2*9 + 1/4^2) – 1 – 9/4
y = 9(x + 1/6)^2 – 13/4
Therefore, the vertex form of y = 9x^2 + 9x – 1 is y = 9(x + 1/6)^2 – 13/4. This form makes it easy to identify the vertex (-1/6, -13/4).
The vertex form allows us to see the transformation of the function from its original form to its vertex form, making it easier to analyze and compare different quadratic functions.
Importance of using Vertex Form in Quadratic Function Analysis
Vertex form is a critical tool for analyzing quadratic functions. Converting a quadratic equation into vertex form helps you identify critical features such as the vertex, minimum or maximum points, and the axis of symmetry.
To convert a quadratic equation from the standard form (y = ax^2 + bx + c) to vertex form (y = a(x – h)^2 + k), use the following steps:
- Step 1: Factor out the coefficient ‘a’ from the first two terms of the standard form equation.
- Step 2: Complete the square by adding and subtracting (b/2a)^2 in the equation.
- Step 3: Simplify and rewrite the equation in vertex form.
For instance, to convert the quadratic function y = 9x^2 + 9x -1 into vertex form, complete the square process as follows:
y = 9(x^2 + x + (1/9)) – 1 – 9(1/9)
y = 9(x+1/3)^2 – 10/3
Thus the vertex form is (y = 9(x+1/3)^2 – 10/3), and the vertex is (-1/3, -10/3). Using vertex form provides a more simplified and efficient way to graph and analyze quadratic functions.
Pro Tip: Converting quadratic functions to vertex form can also help identify transformations on the parent function.
Analyzing Quadratic Functions in Vertex Form
When graphing quadratic functions, it is important to understand the rewritten equation in vertex form. For example, rewriting y = 9×2 + 9x – 1 equation in vertex form can help you visualize and analyze the function’s shape and calculate the vertex of the function.
This article will look at the steps to rewrite this equation in vertex form.
Determining the Vertex and Axis of Symmetry of Quadratic Functions
The equation needs to be in vertex form to determine the vertex and axis of symmetry of quadratic functions. The vertex form of a quadratic equation is y = a(x – h)^2 + k where (h, k) is the vertex of the parabola, and a is a constant that determines the width of the parabola.
To rewrite the quadratic function y = 9x^2 + 9x – 1 in vertex form, complete the square by adding and subtracting the square of half the coefficient of x: y = 9(x^2 + x/2)^2 + (-1 – 9/4). Simplify the equation to y = 9(x + 1/4)^2 – 37/4. Therefore, the vertex is (-1/4, -37/4), and the axis of symmetry is x = -1/4.
Using the vertex form of the equation, you can easily identify the vertex and axis of symmetry of a quadratic function, which aids in producing an accurate graph of the function.
Determining the Maximum or Minimum Point of Quadratic Functions
To determine the maximum or minimum point of quadratic functions, you need to identify the vertex located at the highest or lowest point on the function’s graph. The vertex can be easily found by using the formula (-b/2a, f(-b/2a)) when the quadratic function is in vertex form; f(x) = a(x – h)^2 + k.
We need to complete the square to analyze the quadratic function y = 9x^2 + 9x – 1 in vertex form. First, factor out the leading coefficient of the quadratic term: y = 9(x^2 + x/9) – 1. Then, take half of the coefficient of the linear term, square it, and add and subtract the result inside the parentheses: y = 9(x + 1/6)^2 – 1 – 3/4.
Therefore, the vertex form of the quadratic function is f(x) = 9(x + 1/6)^2 – 3/4, and the vertex is located at (-1/6, -3/4), which is the minimum point on the graph.
Pro tip: Converting quadratic functions into vertex form can simplify calculations and make it easier to identify essential features such as the vertex, maximum or minimum point, intercepts, and symmetry.
Using Quadratic Functions to Solve Real-World Problems
Quadratic functions are essential in solving real-world problems that involve finding a given scenario’s maximum or minimum value. One way to analyze quadratic functions is by converting them into vertex forms, y = a(x-h)^2 + k.
To rewrite the equation y = 9x^2 + 9x – 1 in vertex form, first factor out the 9, giving you y = 9(x^2 + x – 1/9). Next, complete the square by finding the value of “h” and “k.” You can use the formula h = -b/2a and k = f(h), where b and a are the constants in front of x^2 and x, respectively. In this case, h = -1/2 and k = -8/9. Therefore, the equation in vertex form is y = 9(x + 1/2)^2 – 8/9.
Pro tip: Practice solving problems step-by-step to master using quadratic functions in real-world applications.
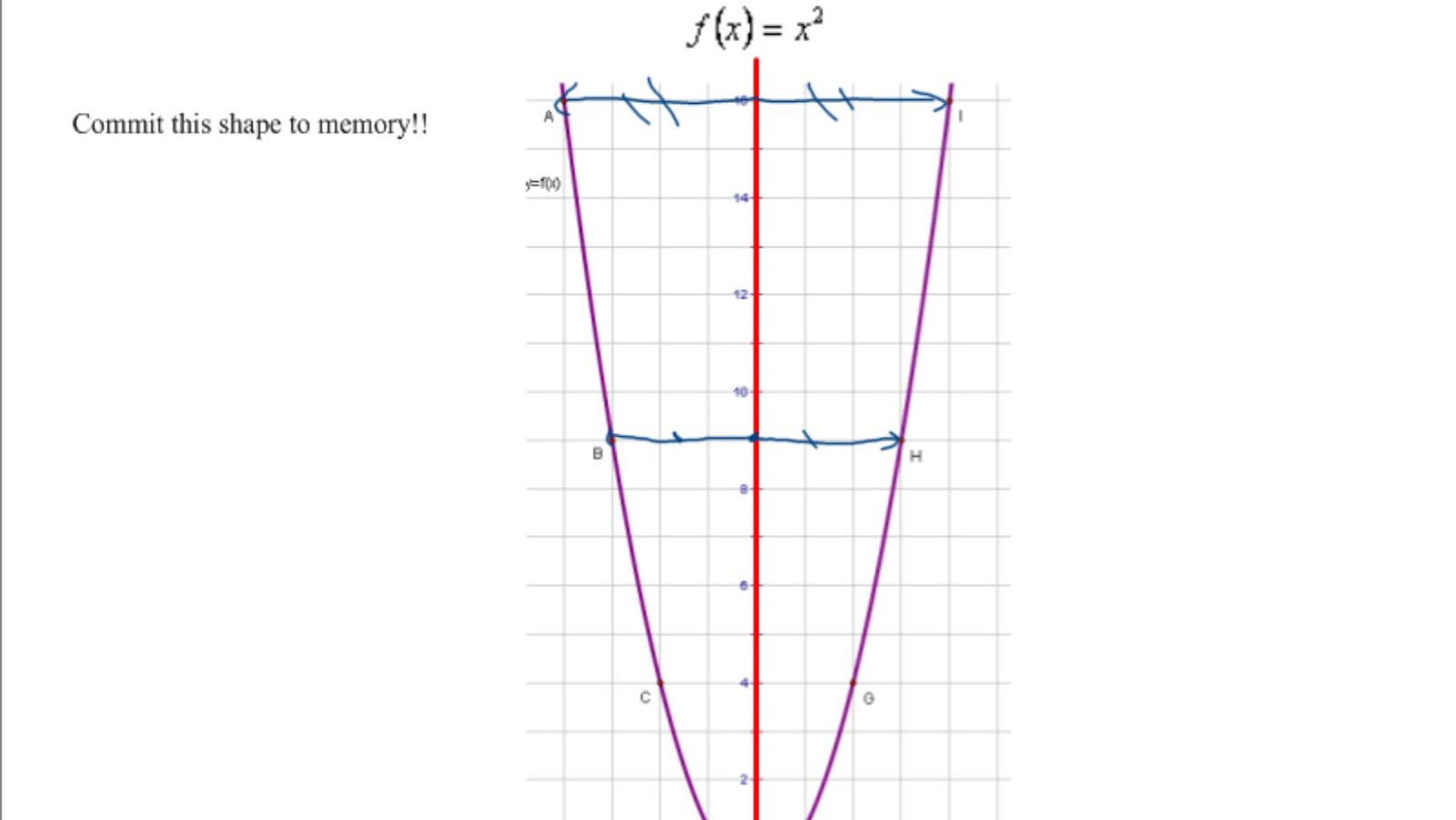
Comparing Quadratic Functions in Different Forms
Quadratic functions can be written in different forms, each with advantages and disadvantages. For example, standard form allows us to easily calculate the roots of the equation, while vertex form allows us to quickly identify the vertex of the parabola.
In this section, we’ll take a look at how to rewrite the equation y = 9×2 + 9x – 1 in vertex form.
Comparing y = ax^2 + bx + c and y = a(x – h)^2 + k forms of Quadratic Functions
Both the quadratic functions, y = ax2 + bx + c and y = a(x – h)2 + k, represent parabolic curves but in different forms.
The vertex form, y = a(x – h)2 + k, is useful when you need to identify the vertex or turning point of a parabola, while standard form, y = ax2 + bx + c, is useful for finding the x- and y-intercepts of a parabola.
We can convert y = ax2 + bx + c into vertex form to compare the two forms. First, we need to complete the square for the x-terms, which involves adding and subtracting (b/2a)2 in the equation.
y = ax2 + bx + c
= a(x2 + (b/a)x)
+ c
Add and subtract (b/2a)2
y = a(x2 + (b/a)x + (b/2a)2 – (b/2a)2)
+ c
Simplify to vertex form
y = a(x – (-b/2a))2 – (b2 – 4ac)/4a
Therefore, y = 9×2 + 9x – 1 can be rewritten in vertex form as y = 9(x + 1/2)2 – 17/4, with the vertex at (-1/2, -17/4).
Though both forms have distinct benefits, knowing how to convert between them allows for greater flexibility when interpreting and manipulating quadratic functions.
Advantages and Disadvantages of Different Forms of Quadratic Functions
Three different forms of quadratic functions exist: standard form, vertex form, and factored form. Each form offers advantages and disadvantages based on the context in which it is used.
Advantages of Standard Form: It explicitly shows a quadratic equation’s coefficients, making it easy to find the x-intercepts and y-intercepts.
Disadvantages of Standard Form: Determining the vertex of the quadratic equation directly from the equation can be challenging.
Advantages of Vertex Form: The vertex form of a quadratic function makes it easy to determine its vertex and shift its position on the coordinate plane.
Disadvantages of Vertex Form: Determining the x-intercepts and y-intercepts of a quadratic equation in vertex form directly from the equation is challenging.
Advantages of Factored Form: It helps to explicitly determine the x-intercepts of a quadratic equation and identify its roots easily.
Disadvantages of Factored Form: Factored form does not give any direct information about the vertex of the quadratic function.
Pro Tip: Each quadratic function form offers unique advantages and disadvantages. Choose the form that best fits your needs and context.
Choosing the Best Form of Quadratic Functions for Specific Applications
The quadratic function y = 9x^2 + 9x – 1 can be rewritten in vertex form as y = 9(x + 1/6)^2 – 1.
Choosing the best form of a quadratic function depends on the specific application and the information you need to extract from the equation.
Standard form (ax^2 + bx + c) is useful for finding the x- and y-intercepts, factoring, and solving quadratic equations using the quadratic formula.
Vertex form (a(x – h)^2 + k) reveals the vertex (h, k) of the parabola and provides information about the minimum or maximum of the function.
Factored form (a(x – r1)(x – r2)) highlights the roots or zeros of the function, i.e., the x-values where the function equals zero.
Understanding the strengths and limitations of each form helps you choose the most appropriate equation depending on the problem at hand. So, always analyze the requirement of the problem before selecting the best form of the quadratic function.